接触第一性计算的时间挺长,但是自己动手算的东西还很少。用mac又不想折腾虚拟机,Materials Studio没法用,所以就把VESTA用起来。
用VESTA建立普通的晶格结构只要知道对称性和原子坐标还是很容易的,但最头疼的是建立表面或者supercell一类要改变原有对称性的体系。
关于VESTA怎么画表面结构,有个很好的网文,“How to Prepare an Input File for Surface Calculations” by Emre S. Tasci。下面讲的基本是按这篇文章的思路,并加入了一些自己的经验。
首先是建立一个普通的晶体结构,我采用的是KTaO3,跟我自己最近的工作有关:)
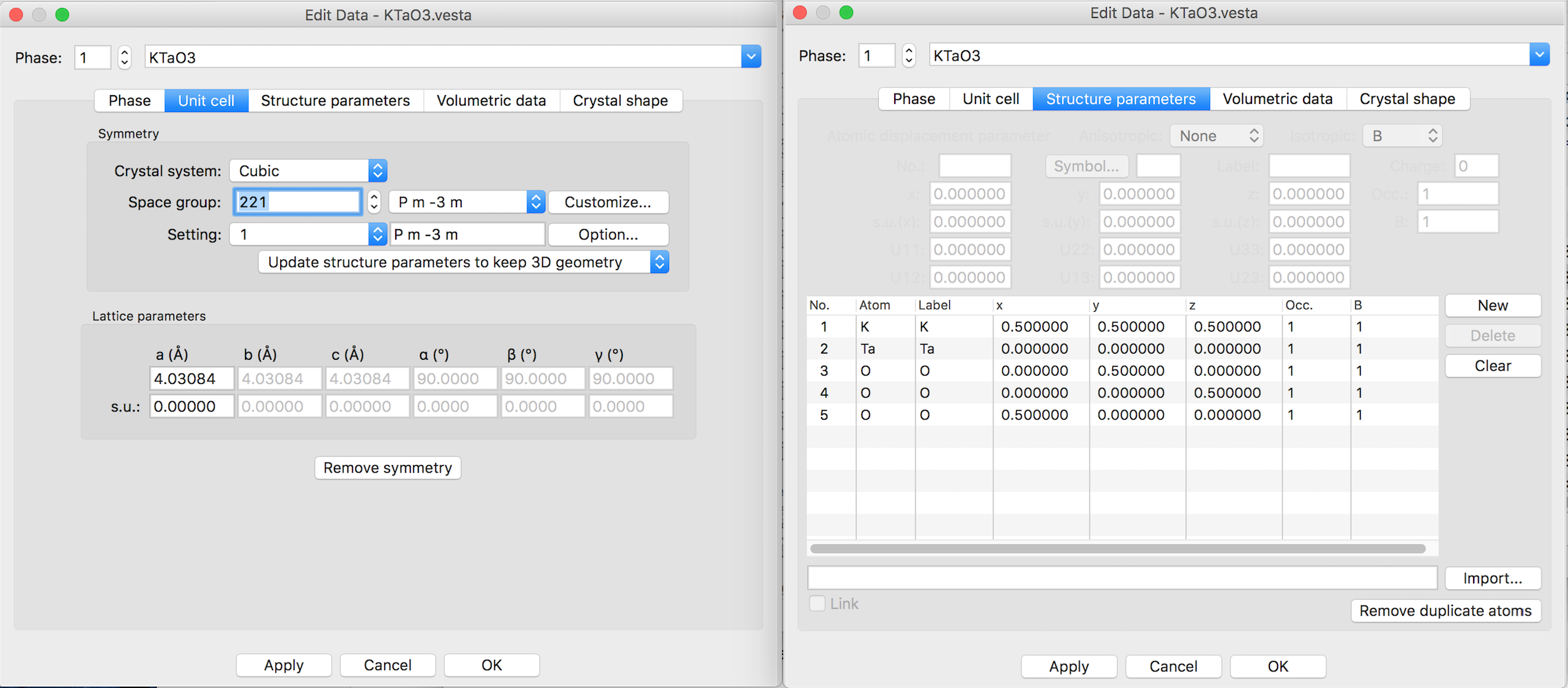
- Edit data>Unit cell
- Crystal system: Cubic
- Space group 221 Pm-3m
- Lattice parameters: a=b=c=4.03084
- Edit data>Structure parameters>New
- K:0,0,0
- Ta:0.5,0.5,0.5
- O:0.5,0,0
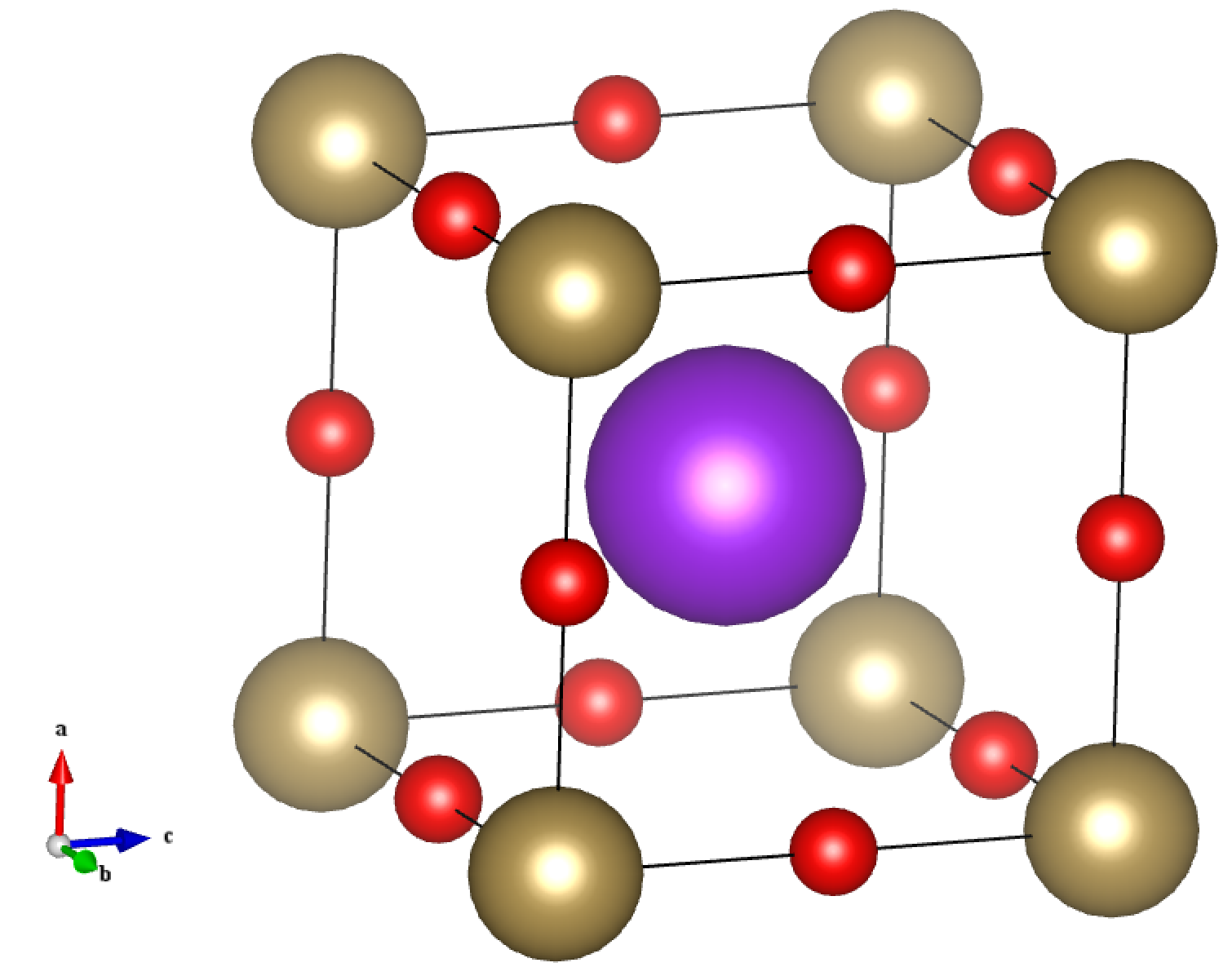
接下来是怎么变晶格的问题,需要在Unit cell>Symmetry>Setting>Option中修改Transformation matrix。对于一般的如(100)表面体系很好处理,仅需要建立一个垂直于表面的supercell。把矩阵里的那三个“1”改改位置,变成想要的层数n就完了。但是处理(111)表面需要旋转,这时候怎么写Transformation matrix就很关键了。
我一开始想的很简单,就是旋转嘛,写个旋转的矩阵就完了。操作起来并不方便,因为三维的时候想得到(111)的旋转操作不是唯一的,还需要稍微算算矩阵。更重要的是结果还不对,原子总是变多或者变少。
后来看了我最开始提到的网文才意识到,变换矩阵是可以根据原来的a,b,c直接写出来的,不怎么需要算。并且这样的结果还保证了合理的晶格形状,结果也才能正确。那么接下来说说我是怎么找的。
其实问题的关键就是要找到变换之后的晶格的矢量,当我准备找(111)面的时候,最简单的一个变换后的矢量是
1 | c' = a+b+c |
这个不用怎么解释。接下来是另外两个矢量。熟悉晶格结构的不用花时间画,不过我不熟悉……。首先是改变boundary(Objects>Boundary)。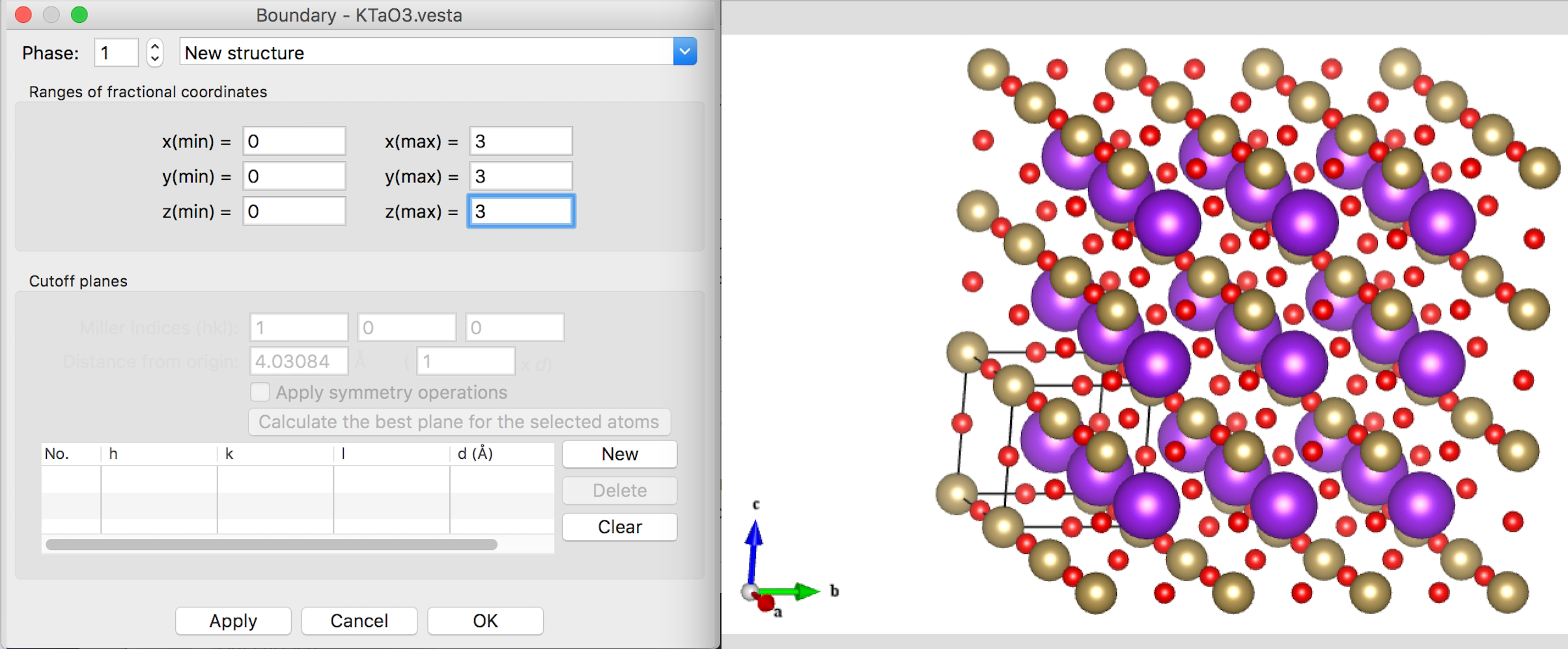
然后选点建立一个(111)截面(Edit>Lattice Planes)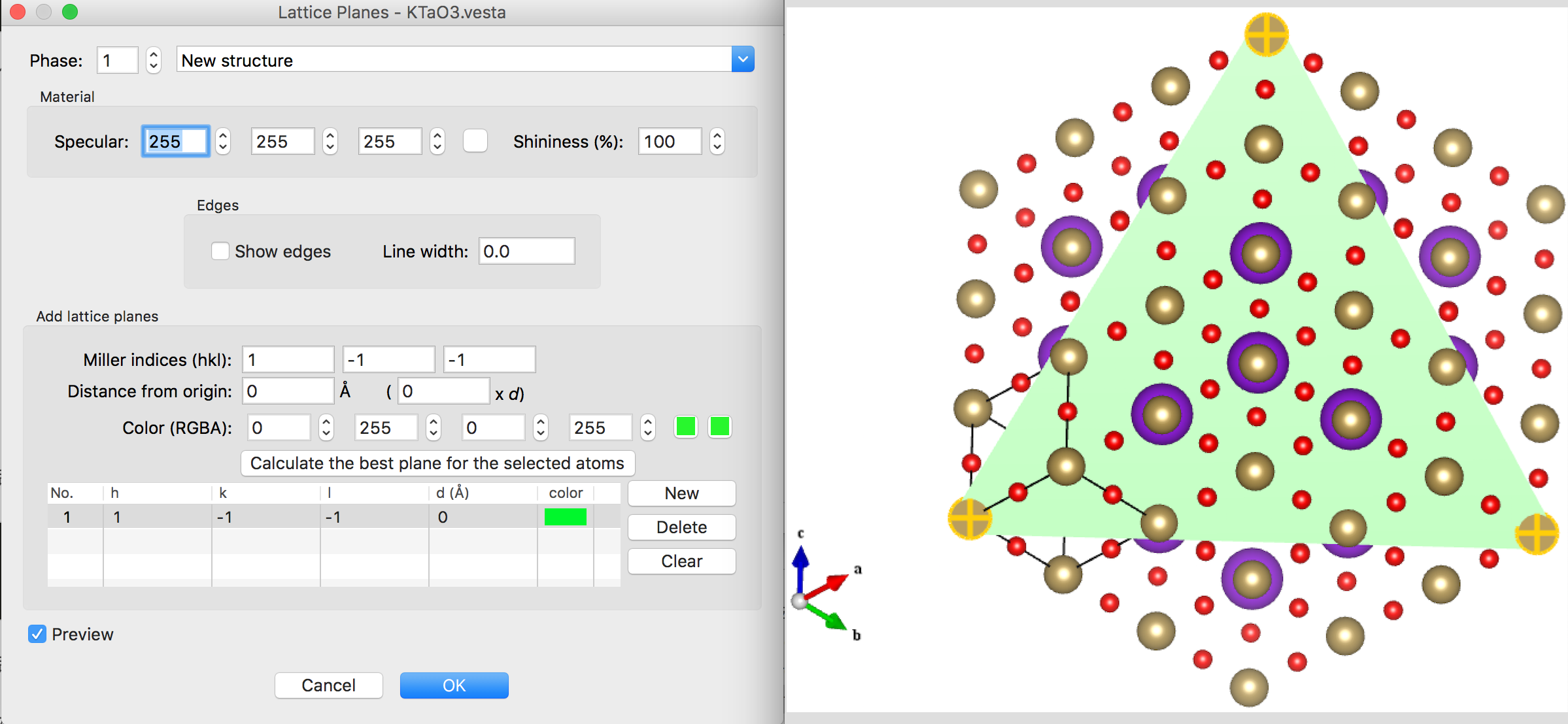
转动去点截面以上的点,我们可以看到露出来的K terminated(111)面。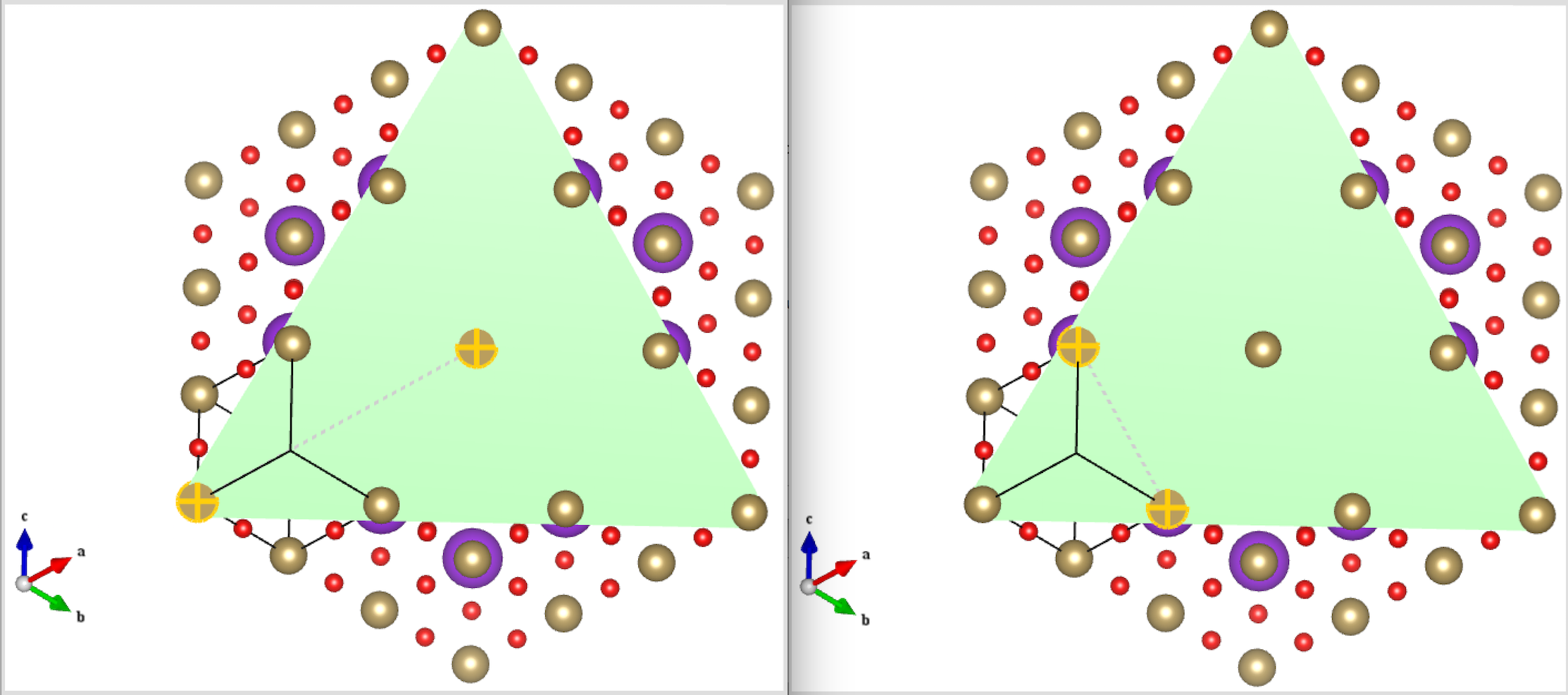
于是另外两个矢量就明显了
1 | b'=(a-c)+(b-c) |
最后,Remove symmetry,把a’,b’,c’矢量竖着填入Transformation matrix就好了(具体可以看下边的补充)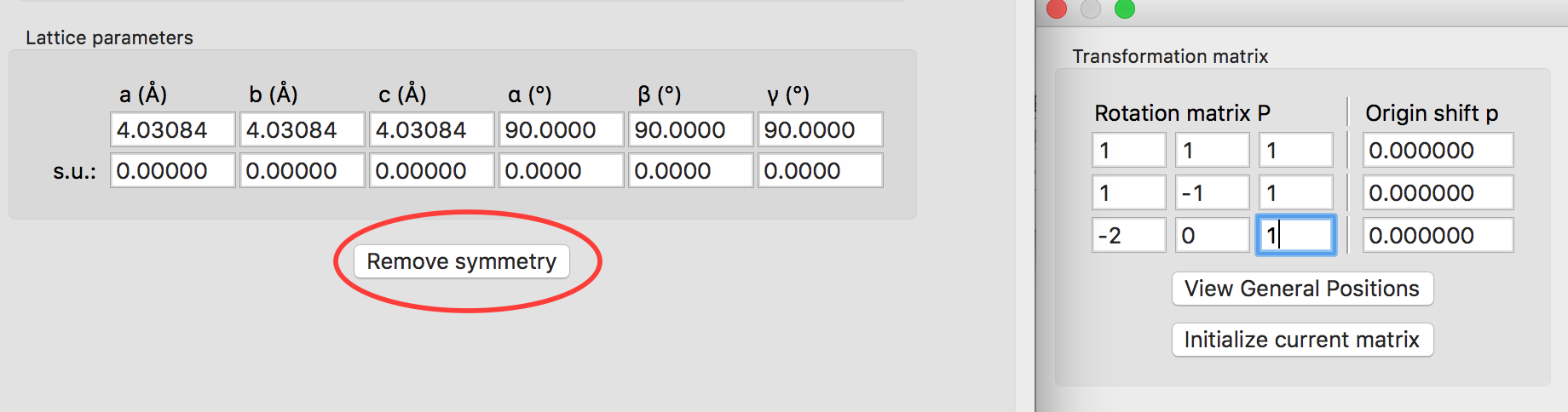
确认matrix的时候会遇到三个warning,我都选了yes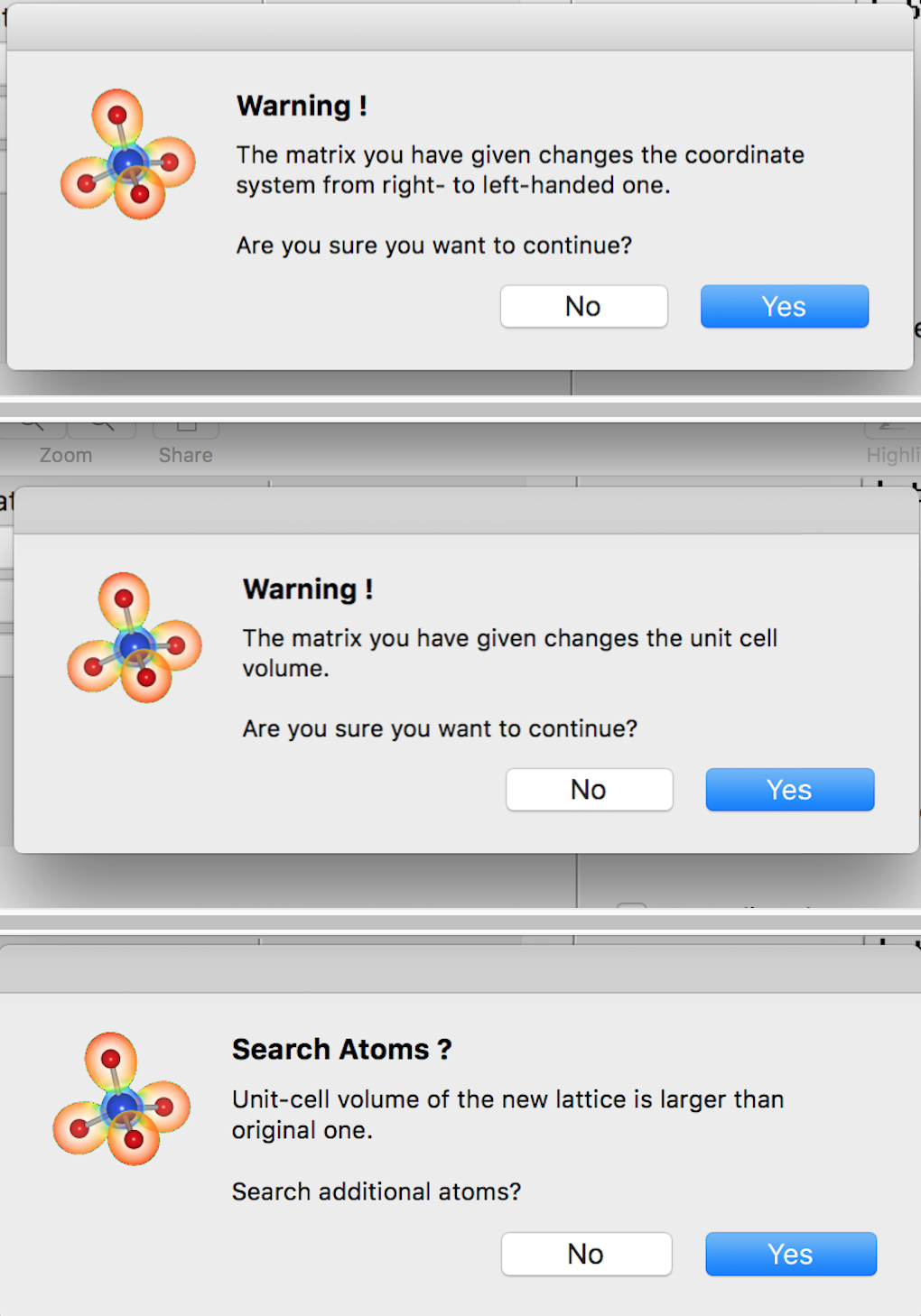
看看我们的结果,和之前的(111)界面是不是一样。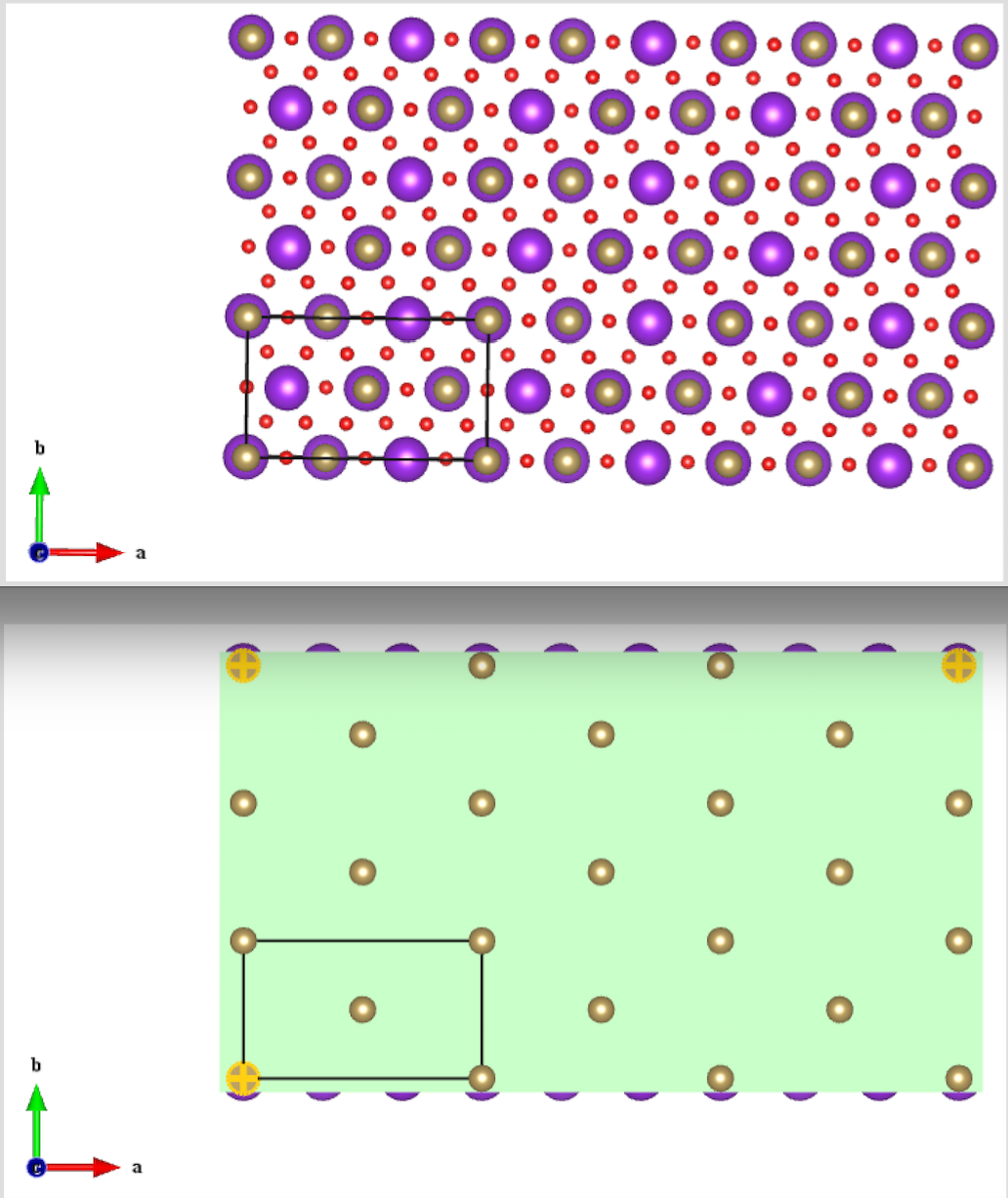
补充:我再总结一下上面的过程和问题。
总体的步骤是:
- 建立完整晶格
- 找到合适的变换后的晶格矢量
- 去掉对称性Edit data>Unit cell>Remove symmetry
- 改变Transformation matrix
- 然后点apply,生成新的结构
关于2和4,最主要是要熟悉寻找的技巧。另外,不要被Manual里边的描述搞晕了,其实你只要想明白通常一开始a,b,c就是(1,0,0),(0,1,0)和(0,0,1),三个矢量也就是个单位矩阵,跟没有一样,所以a’,b’,c’就是你填进去的数字。(我始终不明白很多时候为了严谨性,丢掉了实用性,真的好么?)
关于3,我不知道为什么,但是如果不去掉对称性总是会缺原子,并且即使在Structure parameters里边有的原子也显示不出来。这个求高人指点。